Før man deltar i et spill eller en konkurranse er det vanlig å etablere spillereglene. Hvis man lager reglene etter at spillet er over, kan det sannsynligvis føre til forvirring og uenigheter fordi noen spillere vil foreslå regler som bare ganger dem selv.
I dette blogginnlegget tar vi utgangspunkt i en fotballkamp mellom FC Respons og FC Analyse. Det er allmenn kunnskap at det er fotballaget som skårer flest mål som vinner kampen, men i denne kampen er ikke regelen for kåring av en vinner satt på forhånd. Kampen spilles dog med andre vanlige fotballregler. Når kampen er over skal lagene i fellesskap bli enige om vinneren. FC Respons vil si at de har vunnet fordi de har skåret flest mål (3-1), mens FC Analyse vil si at de har vunnet fordi de har flest skudd på mål (24 versus 3), størst ballinnhav (88 % versus 12%), flest cornere (17 versus 2), flest innkast (19 versus 3) og flest offside (20 versus 2). Se tabell nedenfor.

Siden det i denne kampen ikke var en forhåndssatt regel om hvordan vinneren av kampen skal kåres, foreslo lagene regler som ganget dem selv, og det ble umulig å kåre en vinner. Heldigvis er slike regler satt på forhånd i det virkelige liv for å unngå diskusjoner.
Også i analyse settes det regler for hvordan en «vinner» skal kåres før man starter med datainnsamling.
Videre i innlegget tar vi utgangspunkt i dette scenarioet: 55 personer skal rangere de fem fargene grønn, blå, lilla, rød og oransje fra den fargen de liker best til den fargen de liker minst. Under vises en oversikt over hvor mange som stemte på de ulike fargene som den fargen de likte best:
- 18 personer stemte at de liker grønn best
- 12 personer stemte at de liker blå best
- 10 personer stemte at de liker lilla best
- 9 personer stemte at de liker rød best
- 6 personer stemte at de liker oransje best
Ved bruk av følgende metoder skal vi skal se nærmere på hvordan vi kan få forskjellige «vinnere» med de samme avstemningene:
- Metode 1: Plurality
- Metode 2: Two-Round Runoff
- Metode 3: Instant Runoff
- Metode 4: Borda Count
- Metode 5: Condorcetkriteriet
Metode 1: Plurality
Gjennom plurality kåres vinneren ved å se på det alternativet flest deltakere har valgt som nummer 1. Det er altså bare det alternativet som havner på 1. plass som gjelder. Denne metoden kan sies å være den enkleste matematiske måten å kåre en vinner på.
Som vi ser av oversikten ovenfor, stemte flest personer på grønn som den fargen de liker best. De 18 personene som stemte på grønn som sin favorittfarge satt videre opp rød på andreplass, oransje på tredjeplass, lilla på fjerdeplass og blå på femte- og sisteplass. Se bildet under for full oversikt.

Vinner = GRØNN
Metode 2: Two-Round Runoff
Two-Round Runoff-metoden for å kåre en vinner ligner på Plurality, men plurality gjennomføres to ganger slik at man sitter igjen med en farge som har fått mer enn 1/2 av stemmene.
I mange land – som blant annet Frankrike – velges landets statsleder på denne måten. Det gjennomføres først et valg hvor flere kandidater stiller, og når dette valget er ferdig gjennomføres enda et valg der de to kandidatene som fikk flest stemmer i den første runden får lov til å stille. Dermed vil en av disse kandidatene får mer enn 1/2 av stemmene og kåres som vinneren.
I vårt eksempel med fargene er det kun ett «valg» så vi må simulere «valg» nummer to. I «valg nummer en» får grønn og blå flest stemmer, med 18 og 12 stemmer. I «valg nummer to» teller vi hvor mange som har stemt grønt fremfor blått og hvor mange som har stemt blått fremfor grønt. Med andre ord, hvis de 25 personene som ikke stemte grønn eller blå på førsteplass i første runde (55 personer totalt minus 18 personer som stemte grønn minus 12 personer som stemte blått), måtte velge mellom blå eller grønn, hva hadde de valgt da? I dette tilfellet velger alle 25 blå fremfor grønn, og dermed har blå nå flest førsteplassrangeringer:
- 18 stemte grønn på førsteplass i første valg + 0 nye stemmer i andre valg
= 18 stemmer totalt - 12 stemte blå på førsteplass i første valg + 25 nye stemmer i andre valg
= 37 stemmer totalt

Vinner = BLÅ
Metode 3: Instant Runoff
Ved Instant Runoff går alternativene gjennom flere runder hvor alternativet med lavest antall stemmer elimineres i hver omgang. De stemmene for alternativene som ble eliminert, fordeles deretter på gjenværende alternativer.
Denne metoden brukes blant annet av Oscar-komiteen for å kåre de beste filmene i ulike kategorier.
I vårt eksempel har oransje lavest antall førsteplassrangeringer (6). Av disse seks hadde fire personer blå på andreplass og to personer lilla på andreplass. Dermed øker antall førsteplassrangeringer hos blå med fire og lilla med to. Nå er det da rød som har som har lavest antall førsteplassrangeringer (9), og alle disse ni personene hadde lilla på andreplass. Dermed øker antall førsteplassrangeringer hos lilla med 9. Fortsetter vi med dette i to runder til ender vinneren lilla med 55 førsteplassrangeringer.

Vinner = LILLA
Metode 4: Borda Count
I Borda Count får hver rangering tidelt en poengverdi. Når man multipliserer hver rangering med den tildelte poengverdien og adderer de ulike summene, sitter vi igjen med en verdi som skal sammenlignes med de andre alternativenes verdier. Denne metoden brukes blant annet i flere sportsgrener for å kåre en vinner.
I vårt eksempel har grønn 18 førsteplassrangeringer og 37 femteplassrangeringer. Dermed får grønn (18 x 4)+(37 x 0) = 72 + 0 = 72 poeng. Blå har 12 førsteplassrangeringer, 14 andreplassrangeringer, 0 tredjeplassrangere, 11 fjerdeplassrangeringer og 18 femteplassrangeringer og dermed får blå
(12 x 4)+(14 x 3)+(0 x 2) + (11 x 1) + (18 x 0) = 48 + 42 + 0 + 11 + 0 = 101 poeng. Når vi gjennomfører slike regnestykker for alle de andre fargealternativene også, ender rød opp med flest poeng.

Vinner = RØD
Metode 5: Condorcetkriteriet
En ønsket egenskap ved et valg er Condorcetkriteriet, altså vinnerkandidaten skal slå alle de andre kandidatene i et en mot en-valg. Det vil si at den vinnende kandidaten skal vinne et en mot en-valg, uavhengig av hvem de konkurrerer mot.
Vi ser at oransje vinner en mot en-valget mot samtlige andre farger. For eksempel er den rangert høyere enn grønn ved 19 tilfeller (18 vs. 37 à 37 – 18 = 19).
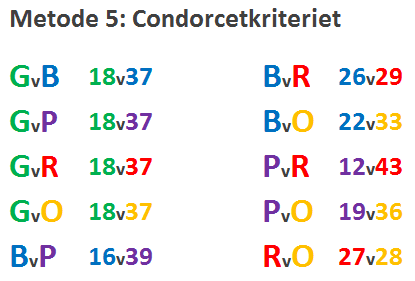
Vinner = ORANSJE
Vi har nå sett at ved bruk av 5 ulike kriterier kan man kåre 5 ulike vinnere med det samme resultatet. Og hver vinner kan rettferdiggjøres. Dette beviser at selv valide tall kan brukes i den retningen man ønsker. Vi ser derfor hvor viktig det er at analysebyråer på forhånd har satt reglene for hvordan tallene skal tolkes. Vet å gjøre dette minimerer man faren for at man kan velge de kriteriene som best gagner ens engen interesse og ikke de kriteriene som best formidler fakta. Noe som på sikt kan føre til et dårlig omdømme for markedsanalysebransjen.
Og hvilken metode jeg synes er den beste?
Alle sammen!
Dette blogginnlegget er basert på Youtube-videon Voting Systems and the Condorcet Paradox av PBS Infinite Series2.
1 https://www.math.ku.edu/~jmartin/courses/math105-F11/Lectures/chapter1-part1.pdf
2 https://www.youtube.com/watch?v=HoAnYQZrNrQ&t=538s
Forfatter
Izat Hanbaly



